Kléopatra est un objet composé essentiellement de fer et de nickel donc de fort albédo.
Son origine est complexe. Il est sans doute le vestige d'un corps beaucoup plus gros, aujourd'hui disparu. Cette planète avortée a subi une fusion totale ou partielle qui a permis le rassemblement en son coeur d'éléments denses comme cela s"est produit pour la Terre.De violentes collisions ont éparpillé ses constituants; les météorites composées de fer et de nickel proviennent aussi du coeur de ces planètes qui n'ont pas survécu aux grandes collisions des premiers temps du système solaire il y a 4,6 milliards d'années..

Sa forme étrange, en forme d'os, est due au rapprochement, en grande douceur, de deux morceaux voisins, de vitesse comparable.

Lors de sa rotation sur lui même, selon la face petite ou grande, qui réfléchit la lumière du Soleil, la luminosité va varier.
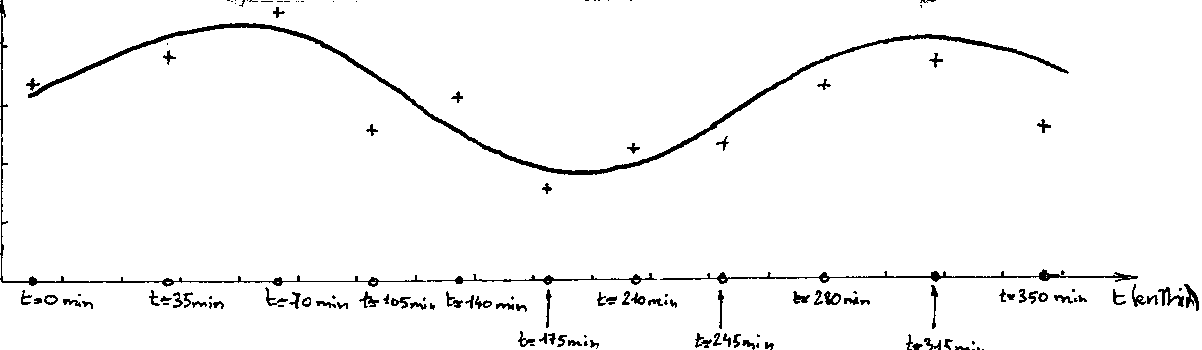
Ainsi, en réalisant la courbe représentant la luminosité en fonction du temps, nous pourrons déterminer la période de rotation propre de l'astéroïde.
 

I) Première approche:Utilisation de l'outil "coupe photométrique" sur les images traitées. Outil "slice"

Les photos sont d'abord prétraitées  ( on retranche le fond de ciel, le "Dark", on divise par une image de "Plage de Lumière Uniforme" ("flat" ou "PLU" )

A côté de l'astéroïde nous choisissons deux étoiles de référence de luminosité intrinsèque constante.

On "normalise"de sorte que la luminosité des étoiles de référence soit constante

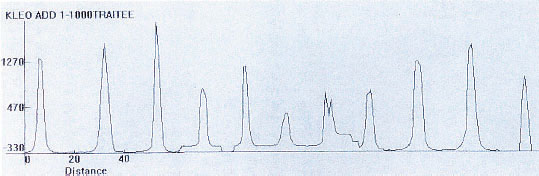
Il nous permet de visualiser le  maximum de luminosité; les photos étudiées étant réalisées à 35 minutes d'intervalle, la turbulence ne varie pas beaucoup   donc la largeur à mi-hauteur de la courbe de luminosité non-plus et la hauteur du pic varie en gros proportionnellement à la luminosité de l'astéroïde

Nous trouvons une période de l'ordre de 4h30
 
 

Avec un peu plus d'attention, on peut mettre en évidence la correspondance entre la taille de la surface présentée et la luminosité de Kléopatra.
En effet, le rapport des valeurs minimale et  maximale de luminosité est égal au rapport des surfaces réfléchissantes de l'astéroïde.
Soient a,b,c les trois dimensions de l'astéroïde assimilé à un parallélépipède, le rapport des surfaces vaut:
Grande surface / petite surface = ab / bc = a / c = éclat max / éclat min = 2,6 / 1,2 = 2,2
or  a = 217 km c = 94 km ce qui donne un rapport de la longueur à la largeur de 2,3
 

 l II) Utilisation de l'outil "Photométrie d'ouverture auto" ou "autoaperture" donnant la luminosité totale de l'astre
Le flux L'astéroïde ou de l'étoile est intégré sur une zone centrée sur l'astre et le fond du ciel est soustrait automatiquement.
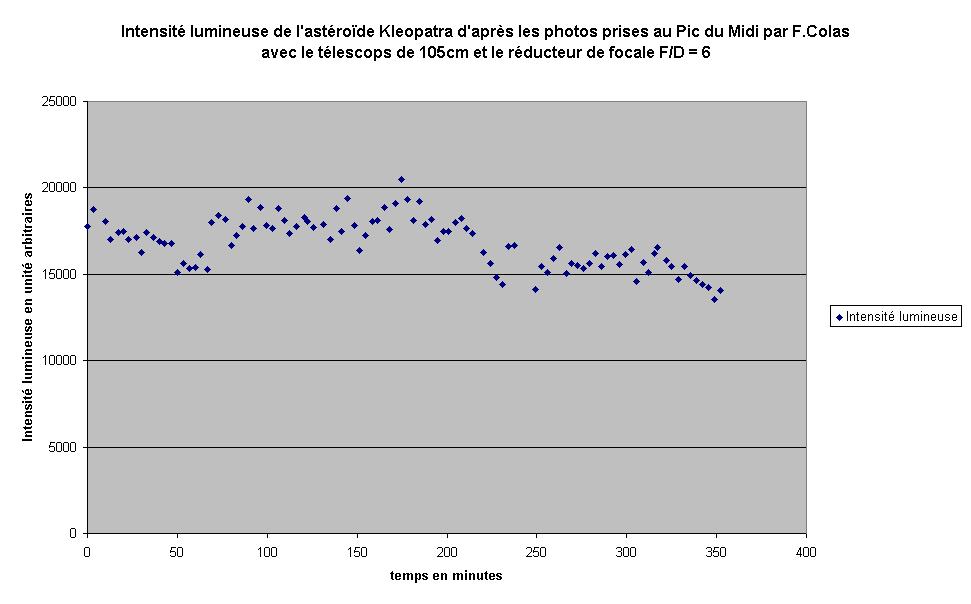
Nous choisissons une centaine de photos prises à environ 3 minutes d'intervalle. Cette fois nous observons des fluctuations..La sinusoïde de l'approche précédente était une approximation grossière; pour conclure à une allure périodique il faudrait traiter un plus grand nombre de photos mais si on admet ce caractère périodique, alors on peut se contenter de retrouver l'ordre de grandeur de la période.: 320min environ donc environ 5h . Les données du catalogue de Lagerkvist et Claesson donnent 0,224386 jours soit 5,4h.

Cependant, la luminosité varie approximativement entre 15000 et 20000 unités et ne nous permet pas de comparer le rapport des éclats aux rapport des surfaces.Il faudrait faire une étude avec plus de photos.

Nous avons bien conscience que notre travail n'est qu'une ébauche mais elle nous a permis de comprendre le phénomène.